Rotations

Block-library: DUBSI

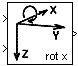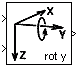
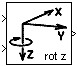
The rotation blocks rotx, roty, and rotz, can be used to express a given vector in terms of a new Cartesian coordinate frame, where the new frame has the same origin as the old, but a different orientation. The three blocks implement transformations for rotations around the positive x, y, and z-axes of a right-handed orthogonal reference system, respectively. The orientation of one three-dimensional reference frame with respect to another can always be described by a sequence of these three plane rotations.

The transformation equation in each of these blocks can be expressed by the following generic vector formula:

(1)

Where u is the input vector, y is the output vector, and T_1—>2 is the transformation matrix; the transformation matrix contains the direction cosines for a rotation from reference frame 1 to reference frame 2.

Let φ, θ, and ψ define the rotations around the x, y, and z-axes, respectively, and let T_φ, T_θ, and T_ψ define the three corresponding rotation matrices. Then the following equations apply: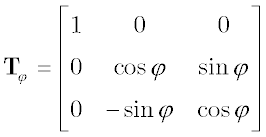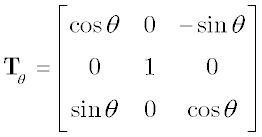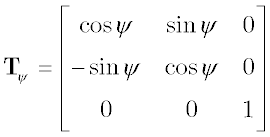

Obviously, rotx implements equation (1) with T_1—>2 = T_φ,  roty uses equation (1)
with T_1—>2 = T_θ, and rotz applies T_1—>2 = T_ψ.

The blocks rotx, roty, and rotz require the following two input signals:

• the three-dimensional vector that needs to be transformed to the new, rotated, reference frame (u = [u₁ u₂ u₃] ^T)
  
  
• the rotation angle φ, θ, or ψ, measured in [rad]

rotx, roty, and rotz do not require any block-parameters. By connecting these blocks in sequence, an arbitrary rotation of the reference frame can be obtained.